Sobre a FMC

A maior parte de nossas pesquisas está associada com a Física da Matéria Condensada, principalmente com o magnetismo. Assim, falaremos brevemente sobre isso, dando enfase aos tópicos que temos trabalhado atualmente. Abaixo, segue um pequeno resumo ilustrado do que é a Física da Matéria Condensada, voltado principalmente para o público leigo.

No mundo quântico, aglomerados de átomos e seus elétrons podem formar diferentes estados da matéria tais como cristais, magnetos, supercondutores etc. Cada um tem seu próprio vácuo e suas próprias excitações… Existem muitos sistemas em Matéria Condensada (MC) que vão dos tradicionais metais (condutores, com “elétrons gordos”), semicondutores e isolantes usuais, aos Supercondutores, superfluidos, Isolantes Topológicos, gás de elétrons em duas dimensões (QHE) etc.

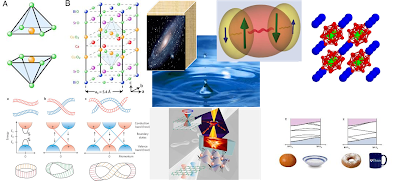
Boa parte de nossos trabalhos está voltada para sistemas de spin… Estes estão associados com o velho, bom e badalado fenômeno do MAGNETISMO: a capacidade de materiais, tais como o Ferro (Fe), de formar magnetos permanentes (tipo imãs) surge do alinhamento espontâneo dos “spins” atômicos (pequeníssimos imãs), quando os átomos interagem entre si. Então, para posicionarmos a Matéria Condensada dentro da Física, comecemos pelos imãs.

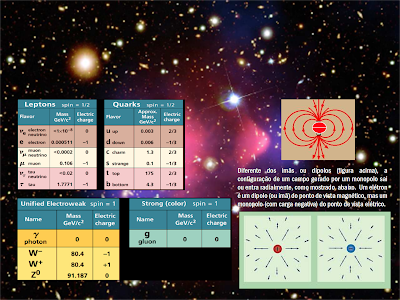
Um fato notável é que um imã possui dois polos, Norte e Sul (por isso eles são conhecidos como dipolos magnéticos). Na figura acima, esses polos são representados pelas cores azul (para o Sul) e vermelha (para o Norte). Estes polos nunca foram observados separados (estão sempre juntos). Isto significa que a tentativa de cortar um imã em duas partes sempre levará a dois novos imãs. A repetição do processo até seu “limite teórico” levará inevitavelmente ao elétron, que também é um pequeno imã. O elétron é considerado (até os dias de hoje) como uma partícula fundamental ou elementar (não pode ser quebrado) e, portanto, seria o menor imã livre na Natureza. O fato dos físicos nunca terem “quebrado” tais dipolos, ou melhor, nunca terem observado um monopolo magnético, isto é, uma partícula ou corpo contendo apenas um dos polos (ou Norte ou Sul), não significa que eles não possam existir; significa apenas que nunca vimos nenhum! Nas figuras abaixo, mostramos imãs e seus campos magnéticos: as linhas de campo partem do polo Norte e sempre caem no polo Sul.

Todo o Universo que conhecemos é formado por partículas fundamentais (ver tabela abaixo) e muitas delas são pequeníssimos imãs (elétrons, quarks etc). Parece que monopolos magnéticos não foram necessários para formar o mundo. Mas a humanidade não sabe quase nada sobre o mundo… Voltemos então ao famoso elétron. Ele é um dipolo magnético (imã) mas é um monopolo, do ponto de vista da eletricidade (monopolo elétrico) e possui, portanto, uma carga elétrica isolada (convencionada negativa; como no caso do magnetismo, na eletricidade também existem dois tipos de polos: um com carga negativa e outro com carga positiva. Mas diferentemente do magnetismo, estes pólos podem se separar) . Estas duas propriedades do elétron (imã e carga elétrica) são responsáveis pela formação da maior parte das coisas ao nosso redor (mesa, maçã, árvore, carro etc). Então voltaremos, abaixo, a descrever esses objetos ao nosso redor.

Toda a matéria (ou quase toda) ao nosso redor pode ser descrita matematicamente pela equação de Schrödinger (ver abaixo)… Essa é a Teoria do Tudo em Matéria Condensada.

A equação de Schrödinger é matematicamente completa. Em princípio, podemos obter todas as propriedades de qualquer sistema de muitos corpos (as coisas ao nosso redor, como mesas, metais, maçãs etc) e suas classificações como isolantes, condutores, semicondutores entre outros!) Entretanto, essa discussão é, na maioria das vezes, inútil!!!!

A “Teoria do Tudo” (Every Thing Theory) seria uma teoria científica hipotética que procuraria unificar, explicar e conectar em uma só estrutura teórica, todos os fenômenos físicos (juntando, por exemplo, a mecânica quântica e a relatividade geral) num único tratamento teórico e matemático. Na corrente principal da física atual, a Teoria do Tudo poderia unificar todas as interações fundamentais da natureza, que são consideradas como quatro: gravitação, a força forte, a força fraca e a eletromagnética. Visto que a força forte pode transformar partículas elementares de uma classe a outra, a teoria de tudo deveria produzir uma profunda compreensão dos vários diferentes tipos de partículas como sendo de diferentes forças. Acima, fazemos uma analogia, dizendo que a Equação de Schrödinger representaria a Teoria do tudo em Matéria Condensada. O grande problema é que não se pode resolver essa equação para um número muito grande de partículas (ler a discussão abaixo).

De fato, com aquela Hamiltoniana H envolvendo “trilhares” e trilhares de partículas, a exigência computacional seria imensa. Na década de 1980, uma estação de trabalho com 32 Mbyte de RAM poderia resolver um sistema com no máximo 11 elétrons interagindo. Mais de 20 anos depois, o “poder” computacional aumentou umas 100 vezes, possibilitando-nos resolver um problema de apenas 13 elétrons. Para se resolver um problema real de 10 elevado a 23 elétrons interagindo, precisaríamos de um poder de computação além de nossa imaginação. Um computador clássico feito de todos os átomos do universo não seria suficiente para tratar tal problema! Portanto, precisamos de novos métodos para estudarmos tais sistemas de Matéria Condensada. Vamos por partes!

Mas mesmo se pudéssemos resolver essa parada….Ainda resta uma pergunta: consideremos o exemplo de um superfluido. Em baixas energias, (~ 1eV) a dinâmica de um superfluido (filme He) é descrita pela Eletrodinâmica Quântica em (2+1)D (teoria emergente), com fônons fazendo o papel de fótons e vórtices o papel das cargas. Então, “imagine” uma civilização vivendo sobre um filme de Hélio (um tipo de flatland com “seres bidimensionais”)… Podemos conjecturar que seus habitantes descobririam primeiro as Equações de Maxwell com fônons e vórtices (uma teoria efetiva para energias da ordem de 1eV)! Talvez, somente muito mais tarde, eles descobririam as excitações originais (átomos de Hélio e elétrons; altas energias e curtas distancias) e a consequente “everything theory” (TOE, 10eV). …Mas a questão é: se resolvêssemos, obteríamos o estado superfluido da TOE (i.e., por resolver a equação de Schrödinger para todos os átomos e elétrons do He)?? More is different?? (emergência, reducionismos???). Não discutiremos isto aqui.

Considere um pedaço de algum material ao seu redor (o seu relógio, por exemplo). Ele pode ter uma pulseira metálica (ouro, por exemplo) ou mesmo isolante (tal como couro). Ambos os materiais citados são formado por uma quantidade enorme de átomos e elétrons, que interagem entre si. Note numa tabela periódica que tais átomos (ouro e carbono ou, em símbolos, Au e C) são muito diferentes. Esta diferença leva a diferentes propriedades dos dois sistemas: os elétrons na pulseira de ouro têm altas tendências a passear enquanto que na de couro, eles preferem ficar parados. Dizemos que no primeiro caso, o sistema é condutor e no segundo, isolante. Em geral, todos materiais metálicos são condutores.

Em um material condutor, as cargas elétricas se movem como se fossem quase livres; assim, podemos facilmente transportá-las de um lado para o outro do material, simplesmente aplicando um campo elétrico. Isto leva a grande parte da tecnologia criada pela humanidade (a eletricidade, na qual a “informação” viaja de um ponto a outro via cargas elétricas). Dentro das suas casas, você usa e abusa dessa tecnologia e faz “mágica” o tempo todo; você faz cargas elétricas se movimentarem aplicando campos elétricos (quando você acende uma lâmpada, liga a TV etc). Neste caso, as cargas se movem em um fio condutor (normalmente de cobre). Mas quem transporta a carga dentro dos condutores? Um fato interessante é que o valor das cargas elétricas em movimento dentro dos condutores é igual a carga do elétron. Então, à primeira vista, os elétrons seriam os carregadores da informação. No entanto, numa descrição mais detalhada, observa-se que a “massa” das “partículas” que carregam essa carga é, em geral, bem maior que a massa do elétron. Mas não existe nestes materiais, e mesmo no Universo, partículas que possuam a carga do elétron e a massa obtida experimentalmente (essa massa depende do material metálico). De fato, estes materiais contém apenas elétrons (que se movimentam) e átomos ou íons (que são fixos e formam a rede cristalina); no Universo existem partículas fundamentais mais pesadas que o elétron e com a mesma carga (muon e Tau são exemplos, mas suas massas são diferentes das observadas nos metais e também elas têm um tempo de vida muito curto). Com certeza não são os muons e taus que carregam as cargas dentro dos condutores. Então, quem faz este trabalho? Que fantasma é este que tem a mesma carga do elétron mas é mais pesado (gordo)? Tal fantasma surge quando muitos corpos interagem. No metal há trilhares e trilhares de trilhares de elétrons e íons. Todas estas partículas interagem através da força elétrica (tipo a lei de Coulomb). No entanto, parece que existem partículas livres (parecidas com “elétrons gordinhos”).

Devido a essa situação estranha, costumamos frequentemente pensar e até mesmo dizer (por questão de simplicidade) que um metal parece com um simples gás de elétrons livres (embora eles estejam “gordos”). A razão dessa idéia funcionar foi primeiramente formulada por Landau em 1956 na sua teoria dos líquidos de Fermi. Ele mostrou que, o que esse quadro está realmente descrevendo é um gás de “quasi-partículas” (tipo-elétron, pois possuem muitas das propriedades dos elétrons), mas que matematicamente, essas quasi-partículas (os “elétrons gordos” citados anteriormente) são de fato, “aproximações intricadas” (de muitos corpos) para os auto-estados do sistema (os auto-estados são as funções (Psi) na equação de Schrödinger; lembramos que não podemos obter soluções exatas para essa equação para um sistema de muitos corpos como este). Tais aproximações ficam melhores à medida que a temperatura (ou outra escala de energia relevante) é reduzida. Tentemos explicar isto de uma maneira grosseira…Imagine um salão lotado de pessoas em uma cerimônia ou festa (como na figura abaixo). Existe pouco espaço para elas se movimentarem com desenvoltura e, portanto, a maioria fica parada conversando com seus amigos laterais (vizinhos no salão). Podemos comparar estas pessoas fixas com os íons de uma rede cristalina. No entanto, existem outras pessoas menos acomodadas, que querem se movimentar, andar, atravessar o salão etc. Estas seriam como os elétrons no metal! No entanto, para andar no salão, estas pessoas em movimento vão esbarrar nas que estão paradas e em outras que estão também se deslocando pelo salão. As conversas, esbarrões e coisas similares são as interações, que acabam fazendo com que a pessoa se desloque muito mais devagar do que poderia, ou mesmo, pretendia. Na ilustração abaixo, isto é representado (meio exageradamente) pelo grupo amarelo. Note que a pessoa que estava atravessando o salão ficou “blindada” pelas demais ao seu redor, de maneira que ela não consegue interagir com outras pessoas mais distantes (que estão em azul na figura). Surge então um ente novo no salão! O grupo amarelo se comporta como um ente (“pseudo-pessoa” ou “quasi-pessoa”) que parece com a pessoa que quis se deslocar, mas bem mais pesada (ou gorda) e, por isso, bem mais lenta. De fato, à medida que um individuo se desloca neste ambiente, ele de alguma forma “arrasta” outros que estão no seu caminho através de conversas, cumprimentos, afagos, esbarrões etc (as “interações”). É claro que num salão lotado, existem muitos outros “grupos amarelos” mas dificilmente se encontram (ou interagem) e cada grupo segue seu caminho. Essa analogia simplória serve para ilustrar o que deve estar acontecendo dentro de um condutor (metal).

Os elétrons dentro de um metal interagem entre si e com os íons fixos na rede cristalina. A interação é relativamente forte e de longo alcance. Assim, quando um elétron se move, ele empurra outros elétrons fazendo com que ele se pareça mais pesado. No final, na bagunça organizada de um sistema de muitos corpos, um dos efeitos da interação é causar um simples aumento da massa do elétron… Neste empurra-empurra, um amontoado de elétrons e íons causam um “bololô” que se comporta como uma partícula independente (denominada quasi-partícula ou pseudo-partícula) muito parecida com o elétron (ela carrega algumas das propriedades mais marcantes do elétron) mas tem uma massa maior e a vantagem de não interagir (mesmo carregando a carga do elétron), pois fica meio que blindada pelo ambiente envoltório. Ela está praticamente livre dentro do metal ! Por isso muitas vezes você poderá escutar a frase: “um metal é um mar de elétrons livres”. Na verdade, não são elétrons livres, mas partículas (ou melhor, pseudo-partículas) tipo elétrons. Em geral, essas pseudo-partículas carregam a carga e o spin do elétron, mas possuem massas diferentes. Essa representação, devida a Landau, é denominada representação do elétron independente (ou elétron único, pois eles não interagem). A descoberta (em 1979) de metais em que o “elétron” parece ser milhares de vezes mais pesado do que o “elétron real” é uma notável confirmação dessa idéia.

O sucesso desse pensamento foi um dos triunfos da Física do Século XX e se tornou um dos paradigmas da Física da Matéria Condensada. Essa teoria dos Líquidos de Fermi de Landau foi aplicada a todos os materiais conhecidos até bem recentemente e funciona porque ela inclui alguns dos efeitos da repulsão dos elétrons, mesmo tratando de um sistema de “elétrons” livres. O uso de uma massa modificada para o elétron é uma maneira pela qual o “quadro do elétron independente” consegue fazer uma mímica dos efeitos dos outros elétrons. Podemos dizer que o transistor e a revolução dos semicondutores são alguns dos “produtos” desse quad

Mas existe ainda mais um paradigma em Física da Matéria Condensada, também devido a Landau. Tentaremos descrevê-lo de maneira simplificada… Outra coisa surpreendente ocorre quando muitos corpos em interação se aglomeram para formar os materiais. Geralmente essa surpresa aparece quando as escalas de energia (ou temperatura) envolvidas no sistema são abaixadas ou diminuídas. Um fato relevante sobre as interações (entre as partículas que formam um material) é que elas, em geral, tentam manter, de alguma forma, o sistema simétrico. A simetria destes sistemas está associada com a idéia de que o sistema não muda sua energia se um parâmetro associado à simetria variar de maneira global (ou seja em todos os pontos do sistema). Por exemplo, se o sistema tiver uma simetria sob rotação, então se o ângulo de rotação mudar pelo mesmo valor em todos os pontos do sistema, nada de diferente ocorre. A seguir, recorreremos à toalha de mesa para tentar esclarecer!

Aqui falarei sobre “parte da física da toalha de mesa”! Imagine uma mesa redonda toda coberta por uma toalha amarela! Imagine também que a situação é vista de cima! A figura abaixo mostra a mesa coberta por uma toalha vista por cima.

Agora gire todos os pontos da toalha pelo mesmo ângulo (digamos, 90 graus). O que acontece? Basicamente nada!!! Tudo permanece com o mesmo visual anterior. Vista de cima a mesa aparece do mesmo jeito que ela estava antes da rotação. Rodar todos os pontos da toalha pelo mesmo ângulo mantém o sistema idêntico. Isso é um tipo de simetria global do nosso exemplo. Além de global, a simetria considerada é também contínua, pois variamos o ângulo sucessiva e continuamente de zero a noventa graus. Esse sistema (toalha) é invariante sob rotação e o parâmetro associado a isto é um ângulo. Este é um exemplo simples de uma simetria e seu parâmetro.

Nos materiais condensados, coisas semelhantes a essa surgem cotidianamente. Como dissemos anteriormente, as interações entre as partículas possuem algum tipo de simetria e o sistema normalmente consegue evidência-lá (matematicamente, estas interações estão presentes na Hamiltoniana H da equação de Schrödinger mencionada anteriormente). No entanto, se abaixarmos a escala de energia apropriadamente (por exemplo, abaixarmos a temperatura do sistema) uma coisa surpreendente ocorre; a simetria desaparece como num passe de mágica! Diz-se que a simetria foi quebrada espontaneamente, ou seja, nenhum agente externo fez isto acontecer; é o próprio sistema que a quebra. Isto gera uma mudança extraordinária nas propriedades do material. Vejamos um caso explicito do que estamos falando. Talvez o exemplo mais simples seja aquele relacionado aos imãs! No magnetismo sempre encontramos bons exemplos.

Ferro, Cobalto, Níquel e alguns dos terras raras (gadolinium, dysprosium) exibem um comportamento magnético singular denominado “Ferromagnetismo” (o nome vem do latim, Ferrum, pois o Ferro é o exemplo mais comum e dramático). Estes materiais ferromagnéticos exibem um fenômeno conhecido por ordenamento de longo alcance, pois os átomos que os formam (Fe, Co, Ni etc) são pequeníssimos imãs (numa linguagem mais científica, eles possuem spin), que interagem de uma maneira tão interessante que os forçam a se alinharem paralelamente. Para termos uma idéia do fenômeno, façamos o seguinte: primeiro, de agora em diante, usaremos o nome spin em vez de imã; segundo, representaremos os spin por uma pequena seta (que aponta numa direção qualquer, ver figura abaixo). Vale a pena dizer que alguns átomos da tabela periódica possuem spin e outros não. Os átomos citados acima são alguns dos exemplos daqueles que possuem spin.

Agora imagine um sistema (uma barra de Ferro por exemplo, ver figura acima) que contém “trilhares” de átomos com spin. Estes spins interagem entre si de maneira muito peculiar. Normalmente, a interação é de curto alcance de forma tal que um spin arbitrário na rede interage apenas com seus vizinhos mais próximos. Além disso, a interação atua fazendo com que dois spins vizinhos prefiram apontar na mesma direção e sentido (paralelamente).

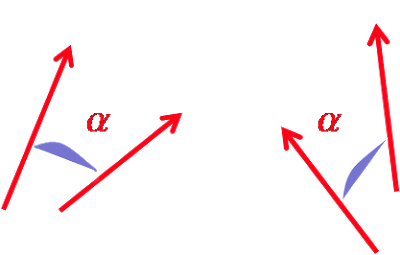
Outro ponto importante a respeito da interação ferromagnética é que ela é simétrica sob rotações, i.e., quando dois spins vizinhos se acoplam, a intensidade da força entre eles depende apenas do ângulo entre eles (ou melhor, do cosseno do ângulo que uma seta faz com a sua vizinha). Então, considere uma configuração qualquer dos “trilhares “ de spins presentes em um ferromagneto. A mudança da direção de todos eles simultaneamente pelo mesmo ângulo não altera a energia total do sistema .

Todas as direções são equivalentes! Se Considerarmos uma situação absolutamente normal, a simetria permaneceria em um ferromagneto se os spins apontassem aleatoriamente em todas as direções possíveis. Como enfatizado anteriormente, os spins vizinhos vão sempre preferir apontar no mesmo sentido para minimizar a energia. E de fato, isso pode ocorrer com todos eles simultaneamente dentro do material se abaixarmos a escala de energia (temperatura) do sistema para um valor compatível com a intensidade da interação. Mas surge, então, a seguinte questão: se todas as direções são equivalentes (devido à simetria), como pode o sistema se ajustar a uma só. Note que se o sistema escolher uma direção particular, a simetria se quebra!

Esse é o ponto principal… Normalmente, quando abaixamos a escala de energia, encontramos uma temperatura (denominada crítica) na qual o sistema começa a “escolher” uma direção particular, desafiando a simetria existente, mas conseguindo uma minimização da energia total envolvida. Abaixo desta temperatura crítica, todos os spins da rede ferromagnética começam a querer apontar na mesma direção; o material como um todo, começa a se transformar num imã (macroscópico) que vai ficando mais forte à medida que a temperatura abaixar ainda mais. Estou falando de um fenômeno que está ocorrendo naturalmente, sem nenhuma interferência de agentes externos (tipo campos magnéticos aplicados externamente etc). Apenas o abaixamento da escala de energia relevante faz com que o sistema passe espontaneamente de uma fase desordenada (com spins apontando aleatoriamente em todas as direções) para uma fase ordenada (com todos spins apontando na mesma direção e sentido), acontecendo, então, a quebra da simetria ressaltada.

Em resumo, o fenômeno descrito é o seguinte: em “altas energias” (temperaturas) o número médio de spins apontando em uma direção (sentido) qualquer é aproximadamente igual ao número médio de spins apontando no sentido oposto. Assim o sistema fica em um estado não-magnetizado (figura acima à esquerda). Quando diminuímos a temperatura para um valor abaixo do crítico, os spins tendem a se alinhar paralelamente (com mais spins apontando em determinado sentido; figura do meio). Finalmente, na temperatura de zero absoluto, todos os spins devem se encontrar perfeitamente alinhados paralelamente (figura à direita), ficando maximamente magnetizado.

A mudança de uma fase desordenada para uma fase ordenada é denominada transição de fase. Este fenômeno é um dos mais importantes em física. As propriedades do sistema são completamente diferentes nas duas fases. Como dissemos anteriormente, esta situação está associada com o segundo paradigma da Física da Matéria Condensada, conhecido como Teoria de Landau das transições de fases (ou quebra de simetria). Ele aponta para o seguinte: as transições de fases estão relacionadas com quebras espontâneas de simetrias. Diferentes fases implicam em diferentes simetrias. Existem muitos outros exemplos de transições de fases em Física, algumas contínuas (como o nosso exemplo), outras não. Mas resumindo nossa presente compreensão sobre estes sistemas de muitos corpos, podemos dizer que a Física da Matéria Condensada “tradicional” se apóia em dois paradigmas devido a Landau. Vamos enumerá-los para efeito de completeza: 1. Teoria de Landau dos Líquidos de Fermi; 2. Teoria de Landau das transições de Fases.

Os dois paradigmas da física do estado sólido (as teorias de Landau dos líquidos de Fermi e das transições de fases) são frutíferos, úteis e têm proporcionado grandes progressos na descrição de metais convencionais, semicondutores, isolantes, magnetos, supercondutores e superfluidos. As idéias relacionadas com o conceito de quasi-partículas como sendo formadas das interações em sistemas de múltiplas partículas, atuando efetivamente como partículas independentes, trouxeram grandes benefícios. De fato, visto que não conseguimos resolver a equação de Schrödinger para os sistemas de muitos corpos (em interação) da matéria condensada, a descoberta de que podemos trabalhar com quasi-partículas independentes (que quase não interagem), facilitou muito os cálculos envolvidos e engrandeceu o nosso entendimento dos comportamentos dos materiais. No entanto, com as descobertas de novos materiais, principalmente a partir dos anos oitenta do século XX, novas idéias e conceitos tornaram-se necessários; estes novos materiais não tinham um comportamento de líquido de Fermi. Além disto, alguns deles podem sofrer transições de fases sem quebras de simetrias. Os dois paradigmas de Landau não conseguem explicar a nova física e novos estados da matéria. Estamos diante de novos desafios e oportunidades!

Os paradigmas de Landau da Física da Matéria Condensada

Existem 2 paradigmas na Física da Matéria Condensada Tradicional devido a Landau:

1. Teoria de Landau dos Líquidos de Fermi
2. Teoria de Landau das Transições de Fases (quebra de simetria).

Falemos primeiro do paradigma 1. É realmente uma surpresa que possamos frequentemente pensar sobre os elétrons em um metal como formando um simples gás de elétrons livres. A razão dessa ideia funcionar foi primeiramente formulada por Landau em 1956 na sua teoria dos líquidos de Fermi. Ele mostrou que, “o que esse quadro está realmente descrevendo é um gás de quasi-partículas (tipo elétron) que possuem muitas das propriedades dos elétrons”, mas que são de fato, aproximações complexas (de muitos corpos) para os auto-estados do sistema. Tais aproximações ficam melhores à medida que a temperatura (ou outra escala de energia relevante) é reduzida.

Esse comportamento pode ser denominado “quadro de um único elétron” (já que não há interação). É claro que existem muitos elétrons em um metal, mas nesse quadro, eles são tratados de maneira que cada um “vivesse” sozinho. O sucesso desse pensamento foi um dos triunfos da Física do Século XX. O transistor e a revolução dos semicondutores são alguns dos “produtos” desse quadro. A teoria funciona porque ela inclui alguns dos efeitos da repulsão dos elétrons, mesmo tratando um sistema de elétrons livres. O uso de uma massa modificada para o elétron é uma maneira pela qual o “quadro de um único elétron” consegue fazer uma mímica dos efeitos dos outros elétrons.

De fato, quando um elétron se move, ele empurra outros elétrons fazendo com que ele se pareça mais pesado. Assim, pelo simples aumento da massa do elétron, é possível incluir alguns dos efeitos da interação. A descoberta (em 1979) de metais em que o “elétron” parece ser milhares de vezes mais pesado do que o “elétron real” é uma notável confirmação dessa idéia.

Agora, falemos sobre o paradigma 2 e outras quasi-partículas! Transição de fase e quebra de simetria: As transições de fases estão relacionadas com quebras espontâneas de simetrias. Diferentes fases implicam em diferentes simetrias. Assim, entendemos as origens de, digamos, fônons sem massa (em super-fluidos). Estão relacionados aos os bósons de Goldstone. Mas o que é quebra de simetria? Por exemplo, uma Hamiltoniana é globalmente invariante sob rotação mas o estado fundamental não exibe essa propriedade… Em magnetismo, mágnons (de spin-1) surgem para restaurar a simetria perdida…

Assim, em magnetismo, quasi-partículas (magnons) surgem acima do estado fundamental …In superfluidos, fônons são as “estrelas” e assim por diante! Eles (magnons e fônons) são as “verdadeiras excitações” (de materiais magnéticos e superfluidos respectivamente). Elas carregam energia e momentum (em geral, pseudo-partículas podem carregar além de energia e momentum, uma carga e um spin).

A ideia de quasi-partículas foi realmente um trunfo na Física da Matéria Condensada (FMC). Em vez de trabalharmos com elétrons e íons, que são muitos e interagem muito fortemente e de maneira complicada e específica, procuramos as “verdadeiras excitações” (quasi-partículas) do vácuo (estado fundamental) do material considerado. Em baixas energias, são elas que se manifestam diretamente nas quantidades observáveis (calor específico, susceptibilidade, função correlação etc). Nada de elétrons e átomos… Existem muitos tipos de quasi-partículas, dependendo do sistema e do vácuo. Elas podem ter ou não gap, podem ser simples e lineares (como mágnons e fônons…) ou até mesmo complexas e não lineares como vórtices e skyrmions.