Sistemas de Spins clássicos em Baixas dimensões

Quando falamos em spin clássico, queremos dizer que consideramos uma aproximação em que o spin (s) do sistema estudado é um vetor tradicional com três componentes obedecendo a um vínculo (a soma do quadrado das três componentes nos dá uma constante). Aplicações desta aproximação podem ser feitas para materiais magnéticos com spins relativamente altos (com valores s=2, s=5/2…) fornecendo excelentes resultados. Cada sistema de matéria condensada possui seu próprio vácuo e suas próprias excitações e, de certa maneira, se comporta como um universo aparte (diferente do “nosso universo”). De fato, as excitações (ou “partículas”) que surgem em matéria condensada não são, em geral, os tradicionais elétrons, fótons, quarks, gluons etc do “nosso universo”. Em geral, elas são diferentes dos “zilhares” de elétrons e íons que formam o material condensado, embora sejam “fabricadas” pela interação e organização destes elétrons e íons. Em vez de se comportarem como partículas independentes, elétrons e íons atuam coletivamente para formar entidades denominadas quasi-partículas, que muitas vezes tem propriedades contra-intuitivas. Um exemplo é o vórtice e seu protagonismo na transição de fase de Kosterlitz-Thouless em sistemas de matéria condensada bidimensionais (magnetos, superfluidos, supercondutores, cristais líquidos etc). Estes tópicos que consideram estados topológicos da matéria estão associados ao Premio Nobel de Física de 2016 (concedido a Haldane, Kosterlitz e Thouless). Sobre, isto, ver também a próxima linha de pesquisa.

Assim, cada material possui sua peculiaridade! Seguindo esta lógica, mencionamos que alguns sistemas de spins clássicos, com spins localizados sobre sítios de redes uni- ou bidimensionais, apresentam uma simetria global e contínua que é quebrada espontaneamente no estado fundamental (vácuo). Se isto acontece, as excitações de mais baixas energias formadas em cima deste vácuo são do tipo bósons de Nambu-Goldstone, que nos sistemas magnéticos, possuem o nome de mágnons (esse é o nome dado à “quase-partícula quântica” associada às ondas de spin). Além de mágnons, excitações (quase-partículas) ainda mais complexas podem surgir;  dependendo de fatores associados aos materiais, como anisotropias ou outras influências, tais quase-partículas (de natureza topológica) são conhecidas como vórtices, solitons etc. Nesta linha de pesquisa, estudamos estas excitações topológicas no campo de spin, suas estabilidades e interações com mágnons,  em redes  com estruturas variadas: redes sem ou com curvaturas (tanto curvatura positiva quanto negativa) ,  redes com configurações defeituosas ou possuindo impurezas etc. Também estudamos transições de fases e o papel das quase-partículas nestas transições e coisas do gênero.  Os modelos mais considerados em nossas pesquisas estão associados ao modelo de Heisenberg e suas variantes como, por exemplo, o modelo XY,  os modelos de Heisenberg  anisotrópicos (tanto de plano-fácil quanto eixo-fácil) etc .

Em nossos estudos, consideramos sistemas magnéticos “clássicos”, de natureza tanto ferromagnética (quando os spins vizinhos tendem a ficar alinhados paralelamente) quanto antiferromagnética (quando os spins vizinhos tendem a ficar alinhados antiparalelamente) e usamos os mais variados métodos para solução dos problemas. Os principais métodos que aplicamos são: teorias de campos (modelo sigma não-linear, bosonização etc) e simulações computacionais (Monte Carlo, diagonalização exata etc).
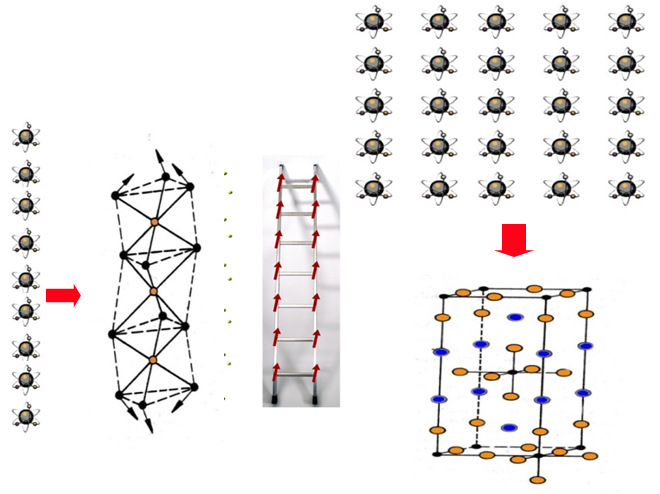
Existem vários compostos exibindo valores de spin que podem ser aproximados por um vetor (clássico). Por outro lado, eles também podem se apresentar em diversas dimensões (ver figura abaixo): materiais magnéticos de zero-Dimensão (0D, “pontolândia”); unidimensional (1D, “linhalândia”); entre uma e duas dimensões (entre 1D e 2D, “escadolândia”); bidimensional (2D, “planolândia”); Tridimensional (3D, “espaçolandia”).